Abstract
We introduce GausSim, a novel neural network-based simulator designed to capture the dynamic behaviors of real-world elastic objects represented through Gaussian kernels. We leverage continuum mechanics and treat each kernel as a Center of Mass System (CMS) that describes continuous piece of matter, accounting for realistic deformations without idealized assumptions. To improve computational efficiency and fidelity, we employ a hierarchical structure that further organizes kernels into CMSs with explicit formulations, enabling a coarse-to-fine simulation approach. This structure significantly reduces computational overhead while preserving detailed dynamics. In addition, GausSim incorporates explicit physics constraints, such as mass and momentum conservation, ensuring interpretable results and robust, physically plausible simulations. To validate our approach, we present a new dataset, READY, containing multi-view videos of real-world elastic deformations. Experimental results demonstrate that GausSim achieves superior performance compared to existing physics-driven baselines, offering a practical and accurate solution for simulating complex dynamic behaviors. Code and model are available at our project page

Methodology
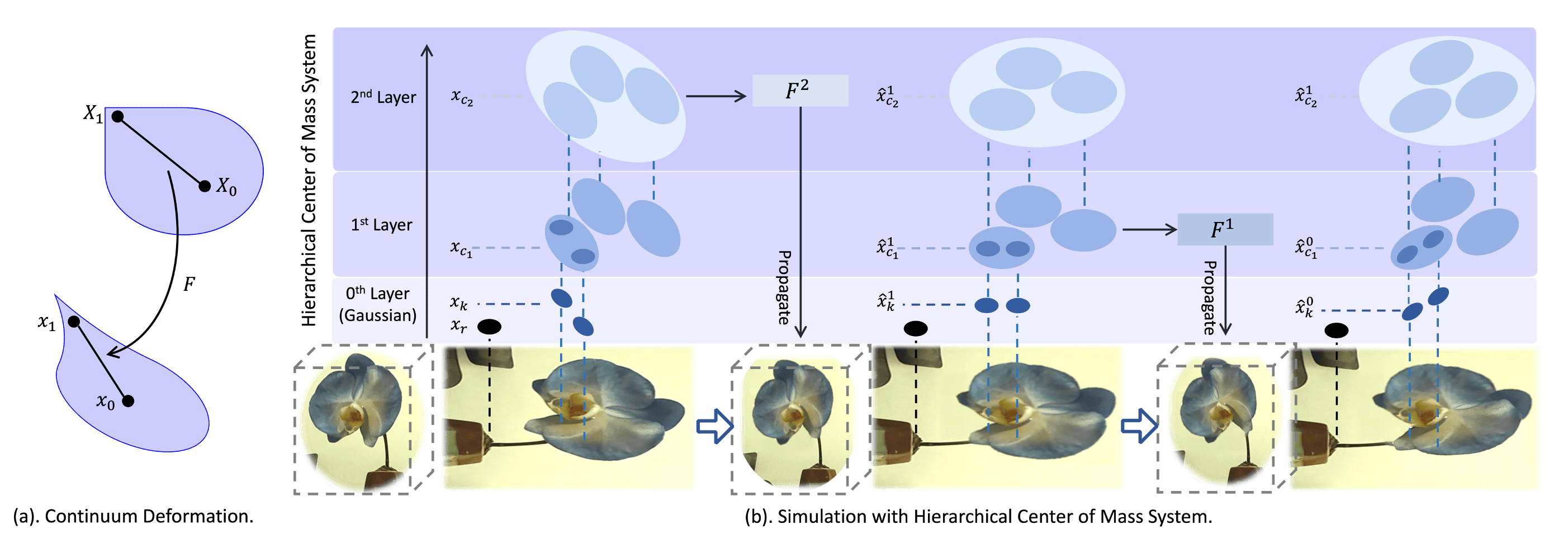
Continuum mechanics is a branch of physics that studies the behavior of materials by modeling them as continuous, rather than discrete, matter. It assumes that materials are continuous and uniform, allowing the analysis of their mechanical behavior (e.g., stress, strain, deformation) under various forces and conditions, which is generally applicable in real world. In this work, instead of discrete particle, we treat each Gaussian kernel as a CMS that describes continuous piece of matter, with a detailed explanation provided in the Appendix. Hence, our approach can model the deformation and dynamics of objects more accurately. This aligns with the principles of continuum mechanics, which focus on how materials respond to forces and deformations in a continuous domain. In the following sections, we explain how this is achievable on objects represented as Gaussian Splatting.